|
8. У лабораторії знаходяться 10 кроликів, з них носіїв вірусу В1 – три, них носіїв вірусу В2 – сім. Навмання взято два кролика. Яка ймовірність того, що: а) обидва кролики, носії вірусу В1; б) обидва кролики, носії вірусу В2; в) обидва кролики, носії різних вірусів?
19. Для участі у студентських спортивних змаганнях виділено із першої групи 4, із другої – 6, із третьої – 5 студентів. Ймовірності того, що студент першої, другої та третьої груп попаде в збірну курсу, дорівнюють відповідно 0,9; 0,7; 0,8. Навмання вибраний студент за результатами змагань попав у збірну курсу. До якої групи найбільш ймовірно належить студент.
30. Схожість насіння певного сорту рослин оцінюється ймовірністю 0,9. Знайти ймовірність того, що:
а) з 8 насінин зійде 6;
б) з 600 насінин зійде 480;
в) з 600 насінин зійде від 480 до 560;
г) відносна частота насінин, які зійдуть, відхиляється по абсолютній величині від її ймовірності на величину, не більшу за 0,02 при 600.
31. Знайти: а) математичне сподівання; б) дисперсію; в) середнє квадратичне відхилення дискретної випадкової величини X з законом розподілу, який задано в таблиці:
|
X
|
10
|
12
|
20
|
25
|
30
|
|
P
|
0,1
|
0,2
|
0,1
|
0,2
|
0,4
|
42. Випадкова неперервна величина X має функцію розподілу 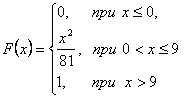 . Знайти: а) щільність розподілу; б) математичне сподівання; в) дисперсію. Побудувати графіки функції розподілу та щільності розподілу. . Знайти: а) щільність розподілу; б) математичне сподівання; в) дисперсію. Побудувати графіки функції розподілу та щільності розподілу.
53. Середня глибина посіву насіння становить 3 см. Окремі відхилення від цього значення випадкові, розподілені нормально з середнім квадратичним відхиленням 0,5 см. Визначити: 1) долю насіння, посіяного на глибину менше 4 см; 2) долю насіння, посіяного на глибину менше 2 см.
64. Добовий надій молока від однієї корови на фермі становить, л:
|
19
|
11
|
19
|
18
|
16
|
17
|
10
|
11
|
12
|
16
|
|
14
|
13
|
19
|
12
|
20
|
13
|
15
|
18
|
18
|
12
|
|
16
|
12
|
15
|
15
|
17
|
16
|
16
|
13
|
15
|
11
|
|
14
|
18
|
14
|
16
|
13
|
15
|
16
|
14
|
15
|
14
|
Необхідно: 1) побудувати інтервальний варіаційний ряд розподілу корів за добовим надоєм молока та гістограму відносних частот; 2) побудувати емпіричну функцію розподілу 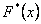 ; 3) визначити точкові незміщені оцінки для ; 3) визначити точкові незміщені оцінки для 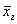 , , 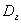 ; 4) знайти моду Mo, медіану Me, розмах варіації R. ; 4) знайти моду Mo, медіану Me, розмах варіації R.
75. Задано середнє квадратичне відхилення 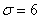 , вибіркове середнє , вибіркове середнє 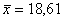 випадкової величини X, яка розподілена нормально, об’єм вибірки n = 81. Необхідно з надійністю випадкової величини X, яка розподілена нормально, об’єм вибірки n = 81. Необхідно з надійністю 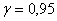 побудувати надійний інтервал для невідомого математичного сподівання a. побудувати надійний інтервал для невідомого математичного сподівання a.
86. Побудувати регресійну модель залежності між товарообігом Z та інтенсивністю потоку покупців P. Обчислити передбачення, якщо прогнозоване значення аргументу P = 14 (тис. чол. в день). Знайти вибірковий коефіцієнт кореляції.
|
Показник
|
Позначення показника
|
Значення показника
|
|
Товарообіг (млн. грн.)
|
Z
|
2,1
|
2,5
|
2,9
|
3,5
|
4
|
4,4
|
5,1
|
5,4
|
|
Інтенсивність потоку покупців (тис. чол. в день)
|
P
|
7
|
7,8
|
8
|
9,8
|
10
|
12,4
|
13,5
|
13,8
|
97. По заданій кореляційній таблиці, яка побудована по результатах вибірки, вибраної з нормально розподіленої генеральної сукупності потрібно:
1) знайти вибірковий коефіцієнт кореляції між X та Y;
2) записати вибіркове рівняння прямої регресії Y на X;
3) з надійністю 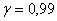 побудувати довірливий інтервал для побудувати довірливий інтервал для 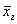 . .
|
Y
|
X
|
ny
|
|
2
|
7
|
12
|
17
|
22
|
27
|
|
10
|
2
|
4
|
|
|
|
|
6
|
|
20
|
|
6
|
2
|
|
|
|
8
|
|
30
|
|
|
3
|
50
|
2
|
|
55
|
|
40
|
|
|
1
|
10
|
6
|
|
17
|
|
50
|
|
|
|
4
|
7
|
3
|
14
|
|
nx
|
2
|
10
|
6
|
64
|
15
|
3
|
n =100
|
| 
