|
6. Прилад складається із трьох незалежно працюючих елементів. Ймовірність виходу із ладу кожного елементу із номером k (k = 1,2,3), дорівнює Pk=0,1+0,05(k-1). Побудувати закон розподілу дискретної випадкової величини Х - числа елементів приладу, які вийдуть із ладу під час його роботи. Обчислити мат. сподівання, дисперсію. Знайти М0 Обчислити F(X).
7. Випадкова величина Х має нормальний закон розподілу із значеннями параметрів 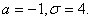 Побудувати графіки функцій f(x), F(x) та обчислити ймовірність подій P (0<X<3), P (|X+1|<4). Побудувати графіки функцій f(x), F(x) та обчислити ймовірність подій P (0<X<3), P (|X+1|<4).
8. Задано щільність двовимірного розподілу неперервної випадкової величини (Х, Y): 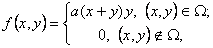 де де 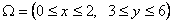 , a - невідомий параметр. , a - невідомий параметр.
Знайти параметр a та коефіцієнт кореляції rxy.
9. За наведеними результатами 50-ти вимірювань значень деякої неперервної випадкової величини Х потрібно:
а) побудувати інтервальний статистичний розподіл вибірки;
б) побудувати гістограму частот та емпіричну функцію розподілу;
в) знайти точкові оцінки математичного сподівання та дисперсії випадкової величини Х;
г) вважаючи, що досліджувана величина Х має нормальний закон розподілу, обчислити теоритичні частоти;
д) за критерієм Пірсона при заданому рівні значущості 0,05 перевірити гіпотезу про узгодженість емпіричних даних з теоретичними;
є) побудувати довірчі інтервали з надійністю 0,95 для невідомих оцінок математичного сподівання і дисперсії;
10. За заданим двовимірним статистичним розподілом вибірки (X,Y) з генеральної сукупності з ознаками 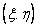 потрібно: потрібно:
а) знайти рівняння вибіркових прямих ліній регресії 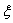 на на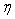 та та 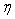 на на 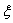 ; ;
б) побудувати графіки одержаних функцій регресії;
в) обчислити умовні середні значення за функціями регресії та за таблицею розподілу;
| 
