 |
Четверг
17.07.2025
03:04 |
| Статистика |
Онлайн всего: 1 Гостей: 1 Пользователей: 0 |
|
|
Приветствую Вас Гость | RSS
Главная | Регистрация | Вход |
| MathHelp 095 689 25 50 Решение контрольных по математике ... |
В категории материалов: 10
Показано материалов: 1-10 |
|
Сортировать по:
Дате ·
Названию ·
Рейтингу ·
Комментариям ·
Просмотрам
Завдання 1.
В першій урні 3 білі та 1 чорна, а в другій – 2 білі та 2 чорні кулі. З першої урни в другу навмання переклали одну кулю, а потім з другої урни взяли одну кулю. Яка ймовірність того, що взята з другої урни куля біла?
Завдання 3.
Випадкова величина Х задана рядом розподілу
Визначити невідому рі. Знайти функцію розподілу випадкової величини F(X) та побудувати її графік. Обчислити математичне сподівання M(X), дисперсію D(X) та середнє квадратичне відхилення σ випадкової величини Х.
Завдання 4.
1. Записати вибірку у вигляді:
· варіаційного ряду;
- статистичного ряду частот;
- статистичного ряду відносних частот.
2. Побудувати полігон, гістограму та кумуляту для вибірки, поданої у вигляді таблиці частот.
3. Обчислити числові характеристики варіаційного ряду розподілу:
· середнє арифметичне значення;
- моду;
- медіану;
- дисперсію;
- середнє квадратичне відхилення;
- коефіцієнт варіації.
4. Пояснити зміст обчислених числових характеристик.
|
1. Во многих странах водительское удостоверение (автомобильные права) имеет шифр, состоящий из 3 букв и 3 цифр. Чему равно общее число возможных номеров водительских удостоверений, считая, что число букв в русского алфавита, используемых для составления шифра, - 26, а буквы занимают первые 3 позиции шифра? Если шифр состоит только из 6 цифр, то чему в этом случае равно общее число всех возможных номеров удостоверений, если: а) цифры в шифре не повторяются? б) если повторяются.
2. Анализ работы кредитного отдела банка выявил, что 12% фирм, бравших кредит в банке, обанкротились и не вернут кредиты, по крайней мере, в течение 5 лет. Также известно, что обанкротились 20% кредитовавшихся в банке фирм. Если один из клиентов банка обанкротился, то чему равна вероятность того, что он окажется не в состоянии вернуть долг банку?
3. Директор компании имеет 2 списка с фамилиями претендентов на работу. В 1-ом списке - фамилии 6 женщин и 3 мужчин. Во 2-ом списке оказались 4 женщины и 7 мужчин. Фамилия одного из претендентов случайно переносится из 1-го списка во 2-й. Затем фамилия одного из претендентов случайно выбирается из 2-го списка. Если предположить, что эта фамилия принадлежит мужчине, чему равна вероятность того, что из 1-го списка была перенесена фамилия женщины?
4. В городе 10 коммерческих банков. У каждого риск банкротства в течение года составляет 10%. Составьте ряд распределения числа банков, которые могут обанкротиться в течение следующего года; постройте график. Найдите числовые характеристики этого распределения. Запишите в общем виде функцию распределения вероятностей и постройте ее график. Чему равна вероятность того, что в течение года обанкротятся не больше одного банка?
5. Дневная добыча угля в некоторой шахте распределена по нормальному закону с математическим ожиданием 785 т и стандартным отклонением 60 т. Найдите вероятность того, что в определенный день будут добыты, по крайней мере, 800 т угля. Определите долю рабочих дней, в которые будет добыто от 750 до 850 т угля. Найдите вероятность того, что в данный день добыча угля окажется ниже 665 т.
6. По данным выборочного обследования получено следующее распределение семей по среднедушевому доходу. Постройте гистограмму распределения частот. Найдите среднедушевой доход семьи в выборке, дисперсию, среднее квадратическое отклонение, коэффициент вариации. Объясните полученные результаты. |
1. Дискретна випадкова величина
X задана таблицею
розподілу. Знайти М(Х), D(X), σ(X), As, Es, інтегральну функцію F(x)
2. Неперервна випадкова Х величина має щільність ймовірностей. Знайти константу з умови нормування.
Знайти M(X), D(X). |
№1. Припустимо, що події A, B, C означають успішне складання іспиту з "Теорії ймовірностей та математичної статистики" першим, другим і третім студентом відповідно. Записати, в чому полягають події: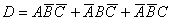 ; ; 
№2. В 3-х банках: "Надра", "Промінвестбанк", "Укрексімбанк" 9 друзів вирішили відкрити по депозитному рахунку. Вважаючи рівно можливим вибір будь-якого банку, знайти ймовірності подій:
а) подія А – у банку "Надра" відкрито рахунок трьома особами;
б) подія В – у одному банку відкрили рахунок рівно 3 особи;
№3. На цирковій виставі рухаються по колу циркового манежу 7 вершників на білих та чорних конях. З них 2 вершники на білих конях. Яка ймовірність того, що вершники на білих конях рухаються один за одним підряд?
№4 На картках написані числа від 60 до 280. Знайти ймовірність того, що число написане на навмання вибраній картці, ділиться:
а) одночасно на 3 та на 5.
б) на 3 або на 5.
№5 У трьох трамвайних вагонах розміщуються 17 пасажирів. Знайдіть ймовірність того, що у першому вагоні розмістяться 7 пасажирів, у другому – 7 пасажирів, у третьому – 3 пасажири.
№6 На потоці 110 студентів: 10 навчається відмінно, 50 – добре, 15 – незадовільно, а решта - трієчники. Ймовірність розв’язання задачі для відмінника – 0,97; для хорошиста – 0,76; для студента, який навчається задовільно – 0,47; для двієчників – 0,16
а) Яка ймовірність розв’язання задачі для навмання обраного студента потоку?
б) Навмання взятий студент не розв’язав задачу. Яка ймовірність, що це хорошист?
№7 Ймовірність того, що впродовж робочого дня не виникне порушень у забезпеченні сировиною дорівнює 0,87. Знайти ймовірність того, що впродовж робочого тижня (5 днів):
а) Порушення будуть впродовж 3 днів;
б) Порушення виникне не більше ніж в 1 день;
в) Знайти найімовірніше число днів без порушень у поставках сировини за робочий місяць (24 дні).
№8 Для вступу до університету необхідно успішно скласти вступні іспити. В середньому їх витримують лише 32 % абітурієнтів. Відомо, що до приймальної комісії подано 2000 заяв. Яка ймовірність того, що принаймні 500 абітурієнтів наберуть прохідний бал?
№ 9 Протягом часу пік (8-00 – 9-30, 17-00 – 19-00) у деякому районі міста відбувається у середньому дві дорожньо-транспортні пригоди за 1 годину.
а) Чому дорівнює ймовірність того, що у деякий день з 8 до 9-30 відбудеться 5 дорожньо-транспортних пригод?
б) Чому дорівнює ймовірність настання 5 дорожньо-транспортних пригод протягом з 17-00 до 19-00?
в) Чому дорівнює ймовірність того, що з 8-00 до 9-30 та з 17-00 до 19-00 однієї доби жодної дорожньо-транспортної пригоди не відбудеться?
№ 10 Дослідний інститут визначив, що 27% виборців підтримують діяльність виконавчої влади. Із великої кількості виборців для участі у телепередачі випадково відібрали 56 осіб. Оцінити ймовірність того, що вибрана доля осіб, які підтримують діяльність виконавчої влади, буде відрізнятись від даних інституту більше ніж на 7%. |
8. Яка ймовірність того, що: а) обидва кролики, носії вірусу В1; б) обидва кролики, носії вірусу В2; в) обидва кролики, носії різних вірусів?
19. До якої групи найбільш ймовірно належить студент.
30. Знайти ймовірність того, що:
а) з 8 насінин зійде 6;
б) з 600 насінин зійде 480;
в) з 600 насінин зійде від 480 до 560;
г) відносна частота насінин, які зійдуть, відхиляється по абсолютній величині від її ймовірності на величину, не більшу за 0,02 при 600.
31. Знайти: а) математичне сподівання; б) дисперсію; в) середнє квадратичне відхилення дискретної випадкової величини X з законом розподілу, який задано в таблиці.
42. Випадкова неперервна величина X має функцію розподілу F(x). Знайти: а) щільність розподілу; б) математичне сподівання; в) дисперсію. Побудувати графіки функції розподілу та щільності розподілу.
53. Визначити: 1) долю насіння, посіяного на глибину менше 4 см; 2) долю насіння, посіяного на глибину менше 2 см.
64.Необхідно: 1) побудувати інтервальний варіаційний ряд розподілу корів за добовим надоєм молока та гістограму відносних частот; 2) побудувати емпіричну функцію розподілу;
75. Необхідно з надійністю 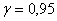 побудувати надійний інтервал для невідомого математичного сподівання a. побудувати надійний інтервал для невідомого математичного сподівання a.
86. Побудувати регресійну модель залежності між товарообігом Z та інтенсивністю потоку покупців P.
97. 1) знайти вибірковий коефіцієнт кореляції між X та Y;
2) записати вибіркове рівняння прямої регресії Y на X;
3) з надійністю 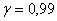 побудувати довірливий інтервал для побудувати довірливий інтервал для 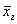 . .
|
1. Скільки різних слів можна скласти з літер вашого а) імені? б) прізвища?
2. Кондуктор автобуса зберігає купюри різної вартості у двох кишенях: в лівій - 7 купюр по 2грн. та 3 купюри по 5 грн., в правій відповідно 12 та 8 купюр. З кожної кишені кондуктор навмання дістає одну купюру. Яка ймовірність того, що: а) обидві купюри однієї вартості? б) купюри різної вартості?
3. На відрізку [-2; 3] навмання вибрано два числа X та Y. Яка ймовірність того, що сума X+Y менша 3, а різниця Y-X менша 2 ?
4. Тираж популярно газети друкується в двох типографіях. Потужності двох типографій відносяться як 3:4, причому перша да 3,5% браку, а друга - 2,5%. Яка ймовірність того, що: а) навмання обраний примірник газети буде бракованим? б) бракований примірник газети надруковано в перший типографії ?
5. Серед 500 коробок взуття нової колекції в 400 лежить взуття чорного кольору. Яка ймовірність того, що у 4 навмання вибраних коробках буде одна з взуттям чорного кольору?
6. У податкових накладних помилки з ймовірністю 5 %. Скільки податкових накладних слід узяти, щоб найімовірніше число накладних без помилок було 70? Яка ймовірність такого числа податкових накладних?
|
1. Бізнесмен проводить чотири фінансові операції з випадковими прибутками (тис. грн.), поданими в таблиці.
По кожній операції бізнесмен несе постійні витрати, подані таблицею.
Потрібно: Побудувати розподіл випадкової величини 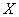 {чистий прибуток}. {чистий прибуток}.
Підрахувати очікуваний середній чистий прибуток (математичне сподівання 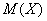 ), дисперсію ), дисперсію 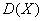 та стандартне відхилення та стандартне відхилення 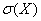 . .
2. Менеджер туристичної компанії виявив, що 30% його клієнтів надають перевагу готелям вищого розряду. Випадковим чином досліджено 8 туристів. Підрахувати ймовірність цієї події:
a) рівно у 5 випадках;
б) число таких випадків знаходиться в межах від 4 до 6.
3. Вага упаковок розфасованого продукту розподілена по нормальному закону із середнім 100 кг і стандартним відхиленням 2 кг. Яка ймовірність, що навмання взята упаковка лежить від 98 до 103 кг.
4. У певний період часу середнє число таксі, що під’їжджають на стоянку на залізничному вокзалі, складає 4 таксі за 5 хвилин. Знайти ймовірність того, що за 5 хвилин під’їде не більше 2 таксі.
5. На біржі було обстежено 600 цінних паперів. За останній місяць 400 з них принесли прибуток. Знайти 95% довірчій інтервал для пропорції прибуткових акцій у генеральній сукупності. |
1. У партії з 10 деталей, 4 браковані. Знайти ймовірність того, що із двох навмання взятих деталей одна стандартна, а одна бракована.
2. На конвеєр подаються деталі з трьох автоматів. Перший дає 90 %, другий – 95 %, а третій 98 % стандартної продукції. Протягом зміни від першого автомата поступає 100 деталей, другого 60 і від третього 40 деталей. Знайти ймовірність попадання на конвеєр стандартної деталі.
3. Задано закон розподілу дискретної випадкової величини.Знайти:
1) значення параметра
2) функцію розподілу, побудувати її графік
3) математичне сподівання та дисперсію випадкової величини
4. Закон розподілу випадкової величини задано функцією розподілу:
Знайти щільність розподілу, та середнє квадратичне відхилення.
5. Випадкова величина розподілена нормально, 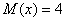 , , 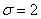 . Знайти імовірності . Знайти імовірності 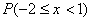 і і 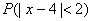 . .
6. За даним статистичним рядом побудувати полігон частот, обчислити 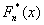 та побудувати графік. та побудувати графік.
7. За даним інтервальним рядом знайти точкові оцінки для математичного сподівання та дисперсії. Вважаючи, що вибірка проведена із нормально розподіленої сукупності з 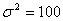 , знайти з надійністю , знайти з надійністю 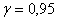 інтервальну оцінку для математичного сподівання сукупності інтервальну оцінку для математичного сподівання сукупності
8. Розв’язати графічним методом:
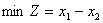 , якщо , якщо 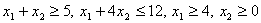 . .
9. Для заданої задачі скласти двоїсту і знайти розв’язок обох задач.
10. Розв’язати транспортну задачу. |
6.1. Дано ймовірності значень випадкової величини: значення 10 має ймовірність 0,3; значення 2 має ймовірність 0,4; значення 8 має ймовірність 0,1; значення 4 має ймовірність 0,2. Побудувати ряд розподілу випадкової величини та многокутник розподілу (полігон).
6.2. Дано ряд розподілу дискретної випадкової величини. Побудувати графік функції розподілу ймовірностей даної випадкової величини.
6.3. Стрілок робить три постріли по мішені. Ймовірність влучення при одному пострілі дорівнює 0,3. Побудувати ряд розподілу числа влучень у мішень.
6.4. В урні 4 кулі з номерами від 1 до 4. Взято дві кулі. Випадкова величина - сума номерів куль. Побудувати ряд розподілу випадкової величини. Знайти функцію розподілу випадкової величини.
6.5. По мішені проведено три постріли. Імовірність влучення в мішень першого пострілу становить 0,1, другого – 0,2, третього – 0,3. Знайти ряд розподілу кількості влучень при трьох пострілах. Побудувати графік розподілу (полігон).
6.6. Серед 5 виробів є один бракований. Щоб його знайти, беруть навмання один виріб за іншим доки не знайдеться бракований. Побудувати ряд розподілу випадкової величини "кількість перевірених виробів".
6.7. Монету кидають 6 разів. Скласти ряд розподілу і побудувати графік розподілу відношення частоти появ герба до числа появ надпису.
6.8. На шляху руху автомобіля 6 світлофорів, кожен з яких дозволяє або забороняє рух автомобіля з ймовірністю 0,5. Скласти ряд розподілу і побудувати функцію розподілу кількості світлофорів, які автомобіль минув до першої зупинки.
6.9. Випадкова величина задана інтегральною функцією. Обчислити імовірність того, що випадкова величина міститься у інтервалі (2,5; 3,5)
6.10. Випадкова величина задана інтегральною функцією. Обчислити імовірність того, що випадкова величина міститься у інтервалі 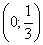 . .
6.11. Випадкова величина задана інтегральною функцією. Знайти щільність розподілу випадкової величини.
6.12. Випадкова величина має закон розподілу зі щільністю.Знайти імовірність того, що випадкова величина попаде у інтервал (1; 2).
6.13. Дано функцію щільності випадково величини. Знайти параметр 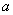 . .
6.14. Випадкова величина задана інтегральною функцією. Звести дану випадкову величину до дискретної та побудувати її ряд розподілу, використовуючи 6 значень дискретної випадкової величини. |
1.22. Гральну кістку підкидають один раз. Яка ймовірність того, що: а) випаде непарне число очок; б) випаде не менше 4 очок; в) випаде не більше 4 очок?
2.22. Підкидають дві гральні кістки, які позначені номерами 1 і 2. Яка ймовірність того, що: а) на першій кістці випаде очок більше ніж на другій; б) на обох кістках випаде однакове число очок.
3.22. Робітник обслуговує три верстати, на яких обробляють однотипні деталі. Ймовірність браку для першого верстату дорівнює 0,02; для другого – 0,03; для третього – 0,04. Оброблені деталі складають в один ящик. Продуктивність праці першого верстата у три рази вища, ніж другого, а третього у два рази менша ніж другого: а) знайти ймовірність того, що навмання взята з ящика деталь бракована; б) деталь яку взяли з ящика виявилась бракованою, знайти ймовірність того, що деталь оброблено на першому, другому і третьому верстатах.
3.22. Робітник обслуговує три верстати, на яких обробляють однотипні деталі. Ймовірність браку для першого верстату дорівнює 0,02; для другого – 0,03; для третього – 0,04. Оброблені деталі складають в один ящик. Продуктивність праці першого верстата у три рази вища, ніж другого, а третього у два рази менша ніж другого: а) знайти ймовірність того, що навмання взята з ящика деталь бракована; б) деталь яку взяли з ящика виявилась бракованою, знайти ймовірність того, що деталь оброблено на першому, другому і третьому верстатах.
4.22. Людина, що належить до певної групи населення, з ймовірністю 0,2 виявляється брюнетом, з ймовірністю 0,3 – шатеном, з ймовірністю 0,4 – блондином і з ймовірністю 0,1 – рудим. Навмання вибирають групу з шести осіб. Знайти ймовірності подій: а) у складі групи не менше 3 блондинів; б) у складі групи хоча б один рудий; в) у складі групи однакове число блондинів і шатенів.
5.22. Серед десяти виготовлених приладів три мають дефект. Знайти закон розподілу і функцію розподілу числа приладів з дефектами серед взятих навмання чотирьох приладів. Обчислити математичне сподівання, дисперсію і середнє квадратичне відхилення цієї випадкової величини.
6.22. Задано вибірку з генеральної сукупності значень дискретної випадкової величини  . Потрібно: а) скласти варіаційний ряд; б) скласти таблицю частот; в) побудувати полігон частот. . Потрібно: а) скласти варіаційний ряд; б) скласти таблицю частот; в) побудувати полігон частот.
7.22. Задано результати 10 спостережень за системою випадкових величин  . Потрібно: а) вважаючи, що залежність між . Потрібно: а) вважаючи, що залежність між  та та  близька до лінійної, знайти за методом найменших квадратів рівняння лінії регресії близька до лінійної, знайти за методом найменших квадратів рівняння лінії регресії  на на  ; б) знайти вибірковий коефіцієнт кореляції ; б) знайти вибірковий коефіцієнт кореляції  . . |
|
|

