 |
Среда
16.07.2025
11:30 |
| Статистика |
Онлайн всего: 1 Гостей: 1 Пользователей: 0 |
|
|
Приветствую Вас Гость | RSS
Главная | Регистрация | Вход |
|
MathHelp 095
689 25 50
Решить контрольную, задачу, пример по высшей математике, теории
вероятности, статистике, математическому моделированию, эконометрии,
маркетингу, экономике предприятия и прочим математическим и экономическим
дисциплинам...
|
Всего материалов в каталоге: 51
Показано материалов: 1-50 |
Страницы: 1 2 » |
Завдання 1.
Споживання палива тепловими електростанціями характеризується даними:
За наведеними даними визначити:
1) обсяги спожитого палива за кожен рік;
2) структуру та структурні зрушення спожитого палива. Зробити висновки.
Завдання 2. (колонки 4, 5)
Основні показники діяльності банків на кінець звітного періоду
За наведеними даними:
1. Згрупувати банки за вказаними ознаками, побудувавши два інтервальні ряди розподілу з рівними інтервалами, виділивши при цьому не менше 3-х груп. Результати подати у вигляді таблиць.
2. Відобразити ряди розподілу графічно.
3. Розрахувати характеристики рядів розподілу:
- середню, моду, медіану;
- середнє лінійне і середнє квадратичне відхилення, дисперсію, коефіцієнт варіації;
- коефіцієнт асиметрії.
4. Побудувати комбінаційний розподіл банків за вказаними ознаками.
Зробити висновки.
Завдання 3.
Обсяги товарних запасів у супермаркеті становили:
Визначити середньомісячні обсяги товарних запасів. Обґрунтувати вибір форми середньої.
Завдання 4.
Задача 1.
Середньорічна кількість працівників в Україні за 2001-2006 рр. характеризується даними, млн. осіб:
Описати тенденцію скорочення кількості зайнятих за допомогою лінійного тренду. Пояснити зміст параметрів рівняння. Результати відобразити графічно. Зробити висновки.
Задача 2.
Використовуючи взаємозв’язок показників динаміки, визначити рівні ряду (кількість зареєстрованих злочинів в Україні за 2001-1006 рр.) і відсутні в таблиці базисні показники динаміки (базис 2001 рік):
Завдання 5.
Задача 1.
За наведеними даними визначити зведений індекс фізичного обсягу виробництва будівельних матеріалів. Пояснити його економічний зміст.
Задача 2.
За даними задачі 1 визначити абсолютний приріст грошових витрат, в тому числі за рахунок зростання фізичного обсягу продукції і за рахунок динаміки собівартості.
Задача 3.
Товарообіг магазину за поточний період зріс на 4.5%, а ціни в середньому знизились на 5%. Як змінився фізичний обсяг продажу?
Задача 4.
За наведеними даними визначити індекси врожайності озимої пшениці змінного і фіксованого складу та структурних зрушень. Пояснити їх економічний зміст.
|
Завдання 1.
В першій урні 3 білі та 1 чорна, а в другій – 2 білі та 2 чорні кулі. З першої урни в другу навмання переклали одну кулю, а потім з другої урни взяли одну кулю. Яка ймовірність того, що взята з другої урни куля біла?
Завдання 3.
Випадкова величина Х задана рядом розподілу
Визначити невідому рі. Знайти функцію розподілу випадкової величини F(X) та побудувати її графік. Обчислити математичне сподівання M(X), дисперсію D(X) та середнє квадратичне відхилення σ випадкової величини Х.
Завдання 4.
1. Записати вибірку у вигляді:
· варіаційного ряду;
- статистичного ряду частот;
- статистичного ряду відносних частот.
2. Побудувати полігон, гістограму та кумуляту для вибірки, поданої у вигляді таблиці частот.
3. Обчислити числові характеристики варіаційного ряду розподілу:
· середнє арифметичне значення;
- моду;
- медіану;
- дисперсію;
- середнє квадратичне відхилення;
- коефіцієнт варіації.
4. Пояснити зміст обчислених числових характеристик.
|
Розрахунково-аналітичне завдання № 8 Використання індексів в економічному аналізі
Завдання: На основі вихідних даних, наведених в табл.7 (згідно варіанта) визначити:
1. Індивідуальні індекси цін та фізичного обсягу виробництва окремих видів продукції.
2. Загальні індекси цін, фізичного обсягу та товарообороту випущеної підприємствами (об’єднанням) продукції.
3. Абсолютну зміну товарообороту за рахунок зміни факторів цін та фізичного обсягу виробництва окремо та разом.
4. Зробити висновки.
Розрахунково-аналітичне завдання № 9 Середньозважені індекси та індекси середніх величин
Завдання: На основі даних, що наведені в табл. 7 (залежно від варіанта), визначити:
1. Загальні індекси фізичного обсягу та цін за формулами середнього арифметичного та середнього гармонічного індексів відповідно (одержані значення порівняти з результатами розрахунково-аналітичного завдання № 8).
2. Зміну середньої ціни (по однорідній продукції двох підприємств), використовуючи індекси структурних зрушень, змінного та фіксованого складу. За результатами розрахунків зробити висновки.
Розрахунково-аналітичне завдання № 10 Статистичні методи вивчення сезонності
Завдання: На основі даних табл.. 8 – 10 визначити:
1. індекси сезонності та побудувати сезонну хвилю;
2. зробити висновки. |
Розрахунково-аналітичне завдання № 6. Аналіз показників динаміки
Завдання : На основі даних табл. 5 та 6 визначити:
1. Абсолютний приріст, темп зростання та темп приросту, а також абсолютне значення 1 % приросту.
2. Середній рівень ряду, а також середні значення абсолютних та відносних показників динаміки.
3. Зробити висновки.
Розрахунково-аналітичне завдання № 7. Аналіз основної тенденції розвитку
Завдання: Дати характеристику основної тенденції розвитку в рядах динаміки за варіантами [див. табл. 5 (варіанти 1—10) та табл. 6 (варіанти 11—20)]. Для цього виконати наступне:
1. Проаналізувати дані динамічного ряду, використовуючи методи укрупнення інтервалів часу та метод плинних середніх.
2. Побудувати рівняння тренду, яке виражає загальну тенденцію зміни рівнів ряду динаміки в часі (за умови, що така тенденція існує), використовуючи метод аналітичного вирівнювання ряду динаміки.
3. Знайти невідомі рівні ряду динаміки (на 5 років), використовуючи метод перспективної екстраполяції. Зробити висновки. |
Розрахунково-аналітичне завдання № 4 Дослідження помилок вибіркового спостереження
Розрахунково-аналітичне завдання № 5 Статистичні методи вивчення кореляційного зв’язку між ознаками (парна кореляція) |
a=7; b=9; c=13
За наведених одночасних показань 20 годинників з однієї партії (у
хвилинах):
16, 25, 34, 7, 25, 43, 25, 34, 7, 34, 43, 52, 25, 34, 34, 16, 43, 25, 16, 34
1. Визначити статистичний розподіл вибірки
1) Утворити дискретний варіаційний ряд і інтервальний варіаційний ряд
2) Знайти і побудувати емпіричну функцію розподілу (кумуляту) і емпіричну щільність частоти (гістограму)
3) Знайти вибіркове середнє, вибіркову дисперсію та центровані і нормовані
варіанти
2. Дати оцінку зазначеного моменту часу з надійністю
(ймовірністю) 0,96
1) класичну (з використанням розподілю Стьюдента)
2) спрощену (з використанням нерівності Чебишева)
3. Сформулювати гіпотезу про розподіл генеральної
сукупності (одночасних показань годинників заданої партії) і перевірити її за
критерієм Пірсона з рівнем значущості 0,04.
|
За наведених одночасних показань 20 годинників з однієї партії (у хвилинах):
16, 23, 30, 9, 23, 37, 23, 30, 9, 30, 37, 44, 23, 30, 30, 16, 37, 23, 16, 30
1. Визначити статистичний розподіл вибірки
1) Утворити дискретний варіаційний ряд і інтервальний варіаційний ряд
2) Знайти і побудувати емпіричну функцію розподілу (кумуляту) і емпіричну щільність частоти (гістограму)
3) Знайти вибіркове середнє, вибіркову дисперсію та центровані і нормовані варіанти
2. Дати оцінку зазначеного моменту часу з надійністю (ймовірністю) 0,94
1) класичну (з використанням розподілю Стьюдента)
2) спрощену (з використанням нерівності Чебишева)
3. Сформулювати гіпотезу про розподіл генеральної сукупності (одночасних показань годинників заданої партії) і перевірити її за критерієм Пірсона з рівнем значущості 0,05.
|
Варіант 1
Задача 1
1. Згрупуйте підприємства за обсягом виручки, виділивши 4 групи з рівними інтервалами. Визначте частку кожної з груп в загальній кількості обстежених підприємств
2. За даними ряду розподілу, побудованому в п.1, визначте характеристики центру розподілу (середню, моду, медіану), а також середньоквадратичне відхилення і коефіцієнт варіації.
Задача 2
Визначте середню частку послуг морського транспорту, обґрунтувавши при цьому вибір виду середньої.
Задача З
1. Обчисліть аналітичні показники ряду динаміки за ланцюговою та базисною системами. Результати подайте у вигляді таблиці.
2. Визначте середньорічну кількість безробітних та середньорічні темпи росту та приросту. Зробіть висновки.
Задача 4За даними задачі 3 опишіть тенденцію зростання доходів страхової компанії лінійним трендом, поясність зміст параметрів трендового рівняння. Припускаючи, що виявлена тенденція збережеться, визначте очікуваний рівень доходів у 2009 р.
Задача 5
1. Визначте зведені індекси : а) цін; б) фізичного обсягу товарообороту, скориставшись системою спів залежних індексів. Поясніть економічну суть отриманих індексів.
2. Розкладіть загальний абсолютний приріст товарообороту за факторами. Зробіть висновки. |
1. Статистичне спостереження. Форми, види спостереження. Вимоги щодо статистичних даних.
2. Дисперсія, суть, види та методи обчислення.
3. Відомі такі дані про випуск валової продукції підприємства:
Знайти базові та ланцюгові темпи зростання і приросту, один відсоток приросту та середньорічний темп зростання.
4. Перевірка готових 500 виробів виявила, що серед них 8 мають дефекти. Визначити з ймовірністю 0,997 довірчі інтервали для частки виробів з дефектом у всій партії 12000 виробів, якщо вибірка є неповторною.
5. Визначити середню заробітну плату працівників підприємства, дисперсію, середнє квадратичне відхилення та коефіцієнт варіації за такими даними:
6. Повна первісна вартість основного капіталу на початок року становила 2500 тис. грн., сума зносу на початок року 150 тис. грн., введено нових основних засобів на 500 тис. грн., вибуло у зв’язку із зносом – 15 тис. грн. (їх повна первісна вартість – 200 тис. грн.). Річна норма амортизації - 8 % . Визначити вартість основного капіталу на кінець року за повною і залишковою вартістю.
|
Варіант 5
1. Середні величини у статистиці. Види середніх величин, умови їх застосування.
2. Загальні індекси та їх взаємозв’язок.
3. Обсяг валової продукції підприємства верстатобудівної промисловості становив 2300 млн грн. Витрати на виробництво становили:
Визначити показники структури та координації витрат на виробництво.
4. Методом випадкової повторної вибірки було взято для перевірки 200 деталей. У результаті перевірки встановлено середню вагу деталей 30 г при середньому квадратичному відхиленні 4 г. Визначити із імовірністю 0,954 межі, в яких перебуватиме середня вага деталей у генеральній сукупності.
5. Визначити тенденцію ряду динаміки прибутку банку методом аналітичного вирівнювання, якщо є такі дані:
6. Є така інформація по області:
Обчислити відносні показники руху населення: коефіцієнти народжуваності, смертності, природного і механічного приросту, життєвості, загальний коефіцієнт приросту, спеціальний коефіцієнт народжуваності.
|
1.3. Систему рівнянь записати в матричній формі та розв’язати методом оберненої матриці та методом Гауса.
2.3. Показати, що перші три вектори утворюють базис тривимірного векторного простору і розкласти вектор за цим базисом (при розв’язанні системи лінійних рівнянь використати формули Крамера).
3.3. Задано координати трьох точок A,B,C. Записати рівняння сторін трикутника AB, AC, BC, висоти AK, знайти кут A і координати точки K.
4.3. Знайти границі функцій:
5.3. Знайти похідну функції:
6.3. Дослідити функцію методами диференціального числення і побудувати її графік.
7.3. Знайти невизначені інтеграли:
8.3. Застосувати визначений інтеграл для обчислення площі фігури, обмеженої заданими лініями:
9.3. Знайти частинні похідні за двома змінними функції двох змінних:
10.3. Знайти загальний розв’язок диференціального рівняння першого порядку й розв’язок задачі Коші для лінійного диференціального рівняння другого порядку.
11.3. Написати перші три члени степеневого ряду і знайти його область збіжності.
|
Варіант 6
1. Середня арифметична проста і зважена, її математичні властивості і спрощені способи обчислення.
2. Ряди динаміки, їх види і основні характеристики.
3. Планом передбачено в поточному році підвищити продуктивність праці на 8 % і зменшити собівартість продукції на 3 %. Фактично продуктивність праці зросла на 10 %, а собівартість виробленої продукції зменшено на 5 %. Визначити рівні виконання плану зі зростання продуктивності праці і зниження собівартості продукції на підприємстві.
4. Визначити базові та ланцюгові темпи зростання і приросту товарообороту, один відсоток приросту товарообороту та середньорічні темпи зростання за такими даними по промтоварному магазину: тис. грн.
5. За даними обстежень домогосподарств житлова площа в розрахунку на одного члена домогосподарства становила:
Визначити середнє значення житлової площі на одного члена домогосподарства, середнє квадратичне відхилення та коефіцієнт варіації. Зробити висновки.
6. У березні щодо січня на ринку було реалізовано молока на 20 % більше при знижені цін на молоко на 20 % за цей період. Обчислити як змінилась виручка від продажу молока у березні щодо січня.
|
Варіант №3
1. Ряди розподілу, їх сутність, види, техніку побудови, графічне зображення.
2. Поняття вибіркового спостереження. Помилки вибіркового спостереження.
3. Відомі такі дані по 24 промтоварних магазинах міста:
……
Побудувати аналітичне групування залежно від продуктивності праці продавців та обсягу товарообороту.
4. Визначити середньозважені індекси цін і кількості проданих акцій на фондовому ринку і зробити висновки за такими даними:
……
5. Чисельність населення міста – 700 тис. осіб. Коефіцієнт природного приросту – 20%, механічного – 30%. Яка чисельність населення передбачається через три роки?
6. За місяць сума явок на роботу дорівнювала 58200 люд.-днів. Сума неявок – 2400 люд.-днів, у тому числі 1300 люд.-днів – святкові і вихідні і 800 люд.-днів чергові відпустки. У кількості явок враховано 210 люд.-днів цілоденних простоїв.
Визначити:
1) календарний, табельний, максимально можливий фонд робочого часу;
2) коефіцієнти використання табельного, максимально можливого фонду робочого часу.
|
З задачи по статистике для КНУТД. Задачи №3, №4, Условие а к задаче 3 (2, 9 варианты). |
З задачи по статистике для КНУТД. Задачи №7, №8, Условие а к задаче 3 (1 вариант). |
Задача 2. Аналітичне групування
Задача 3. Відносні величини динаміки, структури та координації;
Задача 4. За результатами 20% механічної визначити: середній розмір відсоткової ставки, моду, медіану, показники варіації; з ймовірністю 0,997 знайдіть межі, в яких буде знаходитись середній розмір відсоткової ставки в генеральній сукупності; з ймовірністю 0,954 визначте межі, в яких буде знаходитись частка відсоткової ставки в генеральній сукупності для медіанного інтервалу.
Задача 5. Ряди динаміки: ланцюгові і базові абсолютні прирости, темпи зростання і темпи приросту, коефіцієнт прискорення (уповільнення) динаміки; абсолютне значення 1% приросту; середній рівень ряду; середній абсолютний приріст; середньорічні темпи зростання і приросту за 1985-2002 рр.
Задача 6. Середні рівень виробництва холодильників, абсолютний приріст, темп приросту та темп росту. Зробіть висновки щодо типу динаміки.
Задача 7. Індивідуальні індекси кількості та вартості ; загальні індекси кількості та вартості ; проаналізувати зв’язок загальних індексів; обчислити абсолютний приріст вартості в цілому та за рахунок кожного фактору.
Задача 8. Загальний індекс капіталізації; загальний індекс цін; загальний індекс фізичного обсягу куплених акцій. Показати взаємозв’язок індексів; абсолютний приріст вартості акцій в цілому та за рахунок кожного фактора;
Задача 9. За наступними даними визначити середню зміну собівартості продукції по підприємству.
Задача 10. Загальний індекс цін (постійного складу), індекс середньої ціни (змінного складу) та індекс структурних зрушень; зменшення (збільшення) грошової виручки від продажу картоплі за рахунок зміни цін, кількості та структури продажу; зменшення (збільшення) середньої ціни за рахунок зміни цін на окремих ринках міста та структури реалізації; |
6 задач зі статистики на наступні теми:
1. Інтервальний розподіл;
2. Характеристики центра розподілу — середня величина, мода, медіана;
3. Показники варіації для інтервального розподілу: обчислити розмах варіації, середнє лінійне відхилення, дисперсію, середнє квадратичне відхилення, коефіцієнт варіації, а також характеристики форми розподілу — коефіцієнти асиметрії і ексцесу;
4. Наявність і напрямок кореляційного зв'язку між факторною і результативною ознаками методом аналітичного групування;
5. Рівняння регресії, істотність зв’язку за допомогою F критерію;
6. Довірчі інтервали для вибіркового середнього та частки; |
1 ВАРІАНТ
1. Провести групування підприємств за ступенем виконання договірних зобов’язань створивши три групи: до 100%, 100%-105%, 105% і вище. По кожній групі підрахувати:
1) кількість підприємств;
2) фактичний обсяг поставок та з розрахунком;
3) абсолютне відхилення від розрахунків;
4) середній відсоток виконання договірних зобов’язань;
2. Зімкніть динамічний ряд вартості виробничого устаткування фірми, обчисліть базисні абсолютні прирости та темпи приросту. Поясніть зміст розрахованих показників
3. 1. Побудувати баланс використання робочого часу робітників підприємства.
2. Визначити коефіцієнти використання робочого часу.
3. Середню фактичну тривалість робочого дня.
4. Розрахувати:1. Фондоозброєність;2. Механоозброєність праці, якщо середньоспискова чисельність робітників становила 220 чоловік, у тому числі у найбільшій зміні 140 чоловік.
5. 1. Відносну зміну собівартості (загальний індекс змінного складу); 2. Загальні індекси фіксованого складу та структурних зрушень. |
Варіант 4 (Літери Т-Я).
Завдання №1.
На підставі наведених даних:
побудувати групувальну таблицю поділивши сукупність на 3 групи, підрахувати частоти, частки, кумулятивні частоти, кумулятивні частки;
ряд розподілу зобразити графічно
На підставі побудованого ряду розподілу:
розрахувати показники центру розподілу
визначити показники варіації ( R, l, σ, σ2, KR , Kl , Kσ ) ;
на базі коефіцієнтів асиметрії та ексцесу охарактеризувати форму розподілу.
Завдання №2.
Визначити структуру і динаміку товарообороту за рік. Зробити висновки.
Завдання № 3.
Визначити вид ряду динаміки. Обчислити середній рівень ряду, аналітичні показники цього ряду за базисною та ланцюговою схемою. Виявити основну тенденцію явища, а також за умови збереження існуючої тенденції розрахувати прогнозні значення показника на наступні два роки. Зробити висновки.
Завдання № 4
За наведеними даними розрахувати: 1)середню ціну за кожний рік, пояснити причини її розбіжностей; 2) індекси середньої ціни змінного і фіксованого складу та структурних зрушень, пояснити їх економічний зміст. Зробити висновки. |
7 задач по економічній статистиці на наступні теми:
1. Інтервальний розподіл;
2. Середні значення, середня арифметична зважена, середня гармонічна зважена;
3. Показники варіації розподілу отриманого при вибірковому обстеженні: середнє значення, середнє квадратичне відхилення, коефіцієнт варіації, коефіцієнт варіації, мода, медіана, довірчий інтервал для вибіркового середнього;
4. Показники динаміки числового ряду;
5. Індекс: собівартості продукції, фізичного обсягу продукції, витрат на виробництво, собівартості фіксованого складу, собівартості змінного складу, структурних зрушень;
6. Загальний індекс цін;
7. Рівняння регресії, коефіцієнт кореляції, коефіцієнт регресії. |
Задача № 1
Выборочная совокупность задана таблицей распределения. Построить полигон частот. Вычислить несмещенные, состоятельные оценки математического ожидания и дисперсии.
Задача № 2
В таблице представлены результаты телефонных переговоров (в минутах) сотрудников одного из отделов паспортно-визовой службы в течение рабочего дня. Требуется:
- составить интервальный ряд распределения;
- построить гистограмму распределения;
найти несмещенные, состоятельные оценки математического ожидания и дисперсии.
Задача № 3
Дано среднее квадратическое отклонение, выборочная средняя и объем выборки нормально распределенного признака. Найти доверительный интервал для оценки неизвестного математического ожидания с надежностью. |
11 типовых задач по статистике. 1-ый вариант. |
9 задач по статистике. Язык выполнения русский. |
КНЕУ ім. Гетьмана, 2 курс, статистика, 11 варіант
|
Київський національний університет Інститут післядипломної освіти Статистика - 7 варіант (10 задач) |
Київський національний університет Інститут післядипломної освіти Статистика - 6 варіант (7 задач) |
Київський національний університет Інститут післядипломної освіти Статистика - 3 варіант (5 задач)
|
Київський національний університет Інститут післядипломної освіти Статистика - 1 варіант (10 задач)
|
3. Відомі дані про випуск валової продукції підприємства. Знайти базові та ланцюгові темпи зростання і приросту, один відсоток приросту та середньорічний темп зростання.
4. Перевірка готових 500 виробів виявила, що серед них 8 мають дефекти. Визначити з ймовірністю 0,997 довірчі інтервали для частки виробів з дефектом у всій партії 12000 виробів, якщо вибірка є неповторною.
5. Визначити середню заробітну плату працівників підприємства, дисперсію, середнє квадратичне відхилення та коефіцієнт варіації за такими даними:
6. Повна первісна вартість основного капіталу на початок року становила 2500 тис. грн., сума зносу на початок року 150 тис. грн., введено нових основних засобів на 500 тис. грн., вибуло у зв’язку із зносом – 15 тис. грн. (їх повна первісна вартість – 200 тис. грн.). Річна норма амортизації - 8 % . Визначити вартість основного капіталу на кінець року за повною і залишковою вартістю. |
6. Побудувати закон розподілу дискретної випадкової величини Х. Обчислити мат. сподівання, дисперсію. Знайти М0 Обчислити F(X).
7. Випадкова величина Х має нормальний закон розподілу. Побудувати графіки функцій f(x), F(x) та обчислити ймовірність подій
P (4<X<7), P (|X+3|<5).
8. Задано щільність двовимірного розподілу неперервної випадкової величини (Х, Y). Знайти параметр a та коефіцієнт кореляції rxy.
9. За наведеними результатами 50-ти вимірювань значень деякої неперервної випадкової величини Х потрібно: а) побудувати інтервальний статистичний розподіл вибірки; б) побудувати гістограму частот та емпіричну функцію розподілу; в) знайти точкові оцінки математичного сподівання та дисперсії випадкової величини Х; г) вважаючи, що досліджувана величина Х має нормальний закон розподілу, обчислити теоритичні частоти; д) за критерієм Пірсона при заданому рівні значущості 0,05 перевірити гіпотезу про узгодженість емпіричних даних з теоретичними; є) побудувати довірчі інтервали з надійністю 0,95 для невідомих оцінок математичного сподівання і дисперсії;
10. За заданим двовимірним статистичним розподілом вибірки (X,Y): а) знайти рівняння вибіркових прямих ліній регресії; б) побудувати графіки одержаних функцій регресії; в) обчислити умовні середні значення за функціями регресії та за таблицею розподілу;
|
6. Побудувати закон розподілу дискретної випадкової величини Х. Обчислити мат. сподівання, дисперсію. Знайти М0 Обчислити F(X).
7. Випадкова величина Х має нормальний закон розподілу. Побудувати графіки функцій f(x), F(x) та обчислити ймовірність подій
P (-1<X<4), P (|X+4|<2).
8. Задано щільність двовимірного розподілу неперервної випадкової величини (Х, Y). Знайти параметр a та коефіцієнт кореляції rxy.
9. За наведеними результатами 50-ти вимірювань значень деякої неперервної випадкової величини Х потрібно: а) побудувати інтервальний статистичний розподіл вибірки; б) побудувати гістограму частот та емпіричну функцію розподілу; в) знайти точкові оцінки математичного сподівання та дисперсії випадкової величини Х; г) вважаючи, що досліджувана величина Х має нормальний закон розподілу, обчислити теоритичні частоти; д) за критерієм Пірсона при заданому рівні значущості 0,05 перевірити гіпотезу про узгодженість емпіричних даних з теоретичними; є) побудувати довірчі інтервали з надійністю 0,95 для невідомих оцінок математичного сподівання і дисперсії;
10. За заданим двовимірним статистичним розподілом вибірки (X,Y): а) знайти рівняння вибіркових прямих ліній регресії; б) побудувати графіки одержаних функцій регресії; в) обчислити умовні середні значення за функціями регресії та за таблицею розподілу; |
6. Побудувати закон розподілу дискретної випадкової величини Х. Обчислити мат. сподівання, дисперсію. Знайти М0 Обчислити F(X).
7. Випадкова величина Х має нормальний закон розподілу. Побудувати графіки функцій f(x), F(x) та обчислити ймовірність подій
P (0<X<3), P (|X+1|<4).
8. Задано щільність двовимірного розподілу неперервної випадкової величини (Х, Y). Знайти параметр a та коефіцієнт кореляції rxy.
9. За наведеними результатами 50-ти вимірювань значень деякої неперервної випадкової величини Х потрібно: а) побудувати інтервальний статистичний розподіл вибірки; б) побудувати гістограму частот та емпіричну функцію розподілу; в) знайти точкові оцінки математичного сподівання та дисперсії випадкової величини Х; г) вважаючи, що досліджувана величина Х має нормальний закон розподілу, обчислити теоритичні частоти; д) за критерієм Пірсона при заданому рівні значущості 0,05 перевірити гіпотезу про узгодженість емпіричних даних з теоретичними; є) побудувати довірчі інтервали з надійністю 0,95 для невідомих оцінок математичного сподівання і дисперсії;
10. За заданим двовимірним статистичним розподілом вибірки (X,Y): а) знайти рівняння вибіркових прямих ліній регресії; б) побудувати графіки одержаних функцій регресії; в) обчислити умовні середні значення за функціями регресії та за таблицею розподілу; |
Варіант 3
1. Є такі дані про обсяг виготовленої продукції і її собівартість на підприємстві в 2000-2001 рр: Обчислити: 1) загальний індекс фізичного обсягу, собівартості і витрат на виробництво продукції; 2) економічний ефект від зміни собівартості продукції.
2. Динаміка роздрібного товарообороту та цін за регіоном характеризується даними. Визначити: 1) загальні індекси цін і фізичного обсягу товарообороту; 2) абсолютну зміну товарообороту у порівняльних цінах. Зробити висновки.
Варіант 4
1. На біржі нерухомості за добу оформлено продаж 30 трикімнатних квартир, параметри яких наведено в таблиці: За даними таблиці складіть: а) комбінаційний розподіл проданих квартир за двома ознаками (за кожною ознакою виділити по три групи рівних інтервалів): загальна площа – вартість. б) аналітичне групування, яке б описало залежність вартості квартир від їх загальної площі. Результати групувань викладіть у формі статистичних таблиць, проаналізуйте їх, зробіть висновки.
Варіант 7
1. Розподіл проданих на аукціоні держоблігацій за рівнем їх номінальної доходності характеризуються даними: За даними ряду розподілу визначте середнє лінійне відхилення номінальної доходності облігацій.
2. Є дані про товарооборот району (млн. грн.) за 6 років: Необхідно обчислити 1) ланцюгові і базисні: абсолютні прирости; темпи зростання і приросту; абсолютні значення 1% приросту. 2) середній товарооборот продукції за рік, середній абсолютний приріст, середні темпи зростання і приросту.
Варіант 15
2. У 2000 році у світі проживало 48,5 млн. українців. Обчислити відносні величини структури, якщо відомо, що проживало українців (млн. осіб): в Україні – 45,72, в Америці – 1,55, в Канаді – 0,81, в країнах Західної Європи – 0,33, в Австралії – 0,09.
3. Є дані про середньорічну чисельність робітників та службовців в народному господарстві, млн. чол. Обчислити: 1) Скільки службовців приходиться на 100 робітників для 1996, 1997, …, 2000 рр. 2) Динаміку загальної чисельності (базисні відносні величини динаміки). Зробіть висновки.
Варіант 19
2. Магазин у минулому році реалізував товару на 400 тис. грн. Планом на звітний період передбачено реалізувати товарів на 440 тис. грн., а фактично реалізовано на 506 тис. грн. Обчислити відносні величини виконання плану, планового завдання та динаміки.
3. За даними обстежень домогосподарств, житлова площа у розрахунку на одного члена домогосподарства становила, кв. м. Визначте середню житлову площу на одного члена домогосподарства
4. За даними задачі 3 обчисліть моду і медіану.
5. Маємо дані про розподіл сімей за кількістю членів: Обчислити за наведеними даними дисперсію. |
Задача 1. По данным выборки построить ряд распределения. График гистограммы или полигона построить как функцию относительной частоты (частости) с равными интервалами (для гистограммы) признака. Сделать краткие выводы.
Задача 2. По данным своего ряда распределения вычислить характеристики центра распределения - среднюю величину, моду, медиану (для непрерывного признака). Методику вычисления средней величины отобразить в таблицы.
Задача 3. По данным ряда распределения, построенного в задаче 1, вычислить размах вариации, дисперсию, среднее квадратичное отклонение, коэффициент вариации, а также характеристики формы распределения - коэффициенты асимметрии и эксцесса. Расчеты необходимых величин надлежит показать в рабочей таблице. Сделайте выводы.
Задача 4. Принимая исследуемую совокупность (задача 1) за 10% генеральной, определить:
1) с вероятностью 0.997 точечную и граничную ошибки оценки выборочной средней и интервал возможных значений средней величины для генеральной совокупности;
2) точечную ошибку оценки вероятности (частости) первой группы распределения и граничную ошибку этой частости с доверительной вероятностью 0.954, а также границы, в которых она находится в генеральной совокупности;
3) необходимый объем выборки, которая бы обеспечила оценку вероятности (частости) первой группы распределения с точностью до 2% при доверительной вероятности 0.954.
Сделайте выводы.
Задача 5. Выявить наличие и направление корреляционной связи между факторным и результативным признаками для двухмерной выборки. Придать разумный социально-экономический смысл признакам заданной выборки (привести пример). Построить модель аналитической группировки (МАГ) с разделением факторного признака х на 3 равных интервала. Для каждого интервала вычислять групповые средние (левые границы интервалов считать закрытыми, а правые - открытыми), через соответствующие точки провести прямые отрезки. Сделайте выводы о наличии и направлении корреляционной связи.
Задача 6. Оценить тесноту связи в МАГ, которая построена в задаче 5, и проверить ее существенность с уровнем значимости 0,05. Вычислить общую, межгрупповую дисперсию и корреляционное отношение с сведением результатов вычислений в рабочую таблицу. Сделайте выводы о существенности связи.
Задача 7. Для характеристики корреляционной связи между факторным и результативным признаками построить график корреляционного поля и теоретическую модель линейной регрессии (МЛР), которая строится при условии минимизации среднего квадрата ошибки аппроксимации (метод наименьших квадратов – МНК). Определить параметры a и b линейного уравнения регрессии и построить его график. Сделайте краткие выводы. |
1. Знайти вибіркове рівняння лінійної регресії Y на X, вибірковий коефіцієнт кореляції, емпіричну лінію регресії.
2. Знайти вибіркове рівняння лінійної регресії Y на X, вибірковий коефіцієнт кореляції, емпіричну лінію регресії. X - темп народження; Y - доход на душу населення |
Задача 1. Имеются выборочные данные о дневной сборке хлопка (X, кг) вычислить выборочную среднюю, выборочную дисперсию, выборочное среднее квадратическое отклонение этой случайной величины.
Задача 2. Найти доверительный интервал для оценки математического ожидания нормально распределения с надежностью 0,95, зная выборочную среднюю, объем выборки и среднее квадратическое отклонение.
Задача 3. С помощью критерия Пирсона на уровне 0,05 проверить гипотезу о нормальном законе распределения генеральной совокупности Х, если заданы ее эмпирические и теоретические частоты.
Задача 4. Методами корреляционного анализа исследовать зависимость между выпуском продукции Х (тыс. шт.) и себестоимостью одного изделия Y (тыс. руб.) на основе следующих данных. Проверить гипотезу о значимости выборочного коэффициента корреляции при заданном уровне значимости 0,05. Построить линейные уравнения регрессии.
|
Завдання 1. Встановити чи існують відмінності між двома вибірками у рівні досліджуваної ознаки, використавши відповідні статистичні критерії.
Завдання 2.
1. Обчислити коефіцієнт Юла Q.
2. Обчислити коефіцієнт контингенції Ф.
3. Перевірити на значимість.
4. Зробити висновки про ступінь взаємозв’язку між ознаками
|
Работа выполнена в Excel с подробным описанием хода решения и всеми выводами в Word.
Завдання 1. Побудова та частотний і графічний аналіз рядів розподілу.
Завдання 2. Статистичні характеристики центру розподілу
Завдання 3. Статистичні характеристики варіації і форми розподілу
Завдання 4. Метод аналітичного групування і однофакторний дисперсійний аналіз
Завдання 5. Однофакторний кореляційно-регресійний аналіз
Завдання 6. Аналіз рядів динаміки і прогнозування |
1. Во многих странах водительское удостоверение (автомобильные права) имеет шифр, состоящий из 3 букв и 3 цифр. Чему равно общее число возможных номеров водительских удостоверений, считая, что число букв в русского алфавита, используемых для составления шифра, - 26, а буквы занимают первые 3 позиции шифра? Если шифр состоит только из 6 цифр, то чему в этом случае равно общее число всех возможных номеров удостоверений, если: а) цифры в шифре не повторяются? б) если повторяются.
2. Анализ работы кредитного отдела банка выявил, что 12% фирм, бравших кредит в банке, обанкротились и не вернут кредиты, по крайней мере, в течение 5 лет. Также известно, что обанкротились 20% кредитовавшихся в банке фирм. Если один из клиентов банка обанкротился, то чему равна вероятность того, что он окажется не в состоянии вернуть долг банку?
3. Директор компании имеет 2 списка с фамилиями претендентов на работу. В 1-ом списке - фамилии 6 женщин и 3 мужчин. Во 2-ом списке оказались 4 женщины и 7 мужчин. Фамилия одного из претендентов случайно переносится из 1-го списка во 2-й. Затем фамилия одного из претендентов случайно выбирается из 2-го списка. Если предположить, что эта фамилия принадлежит мужчине, чему равна вероятность того, что из 1-го списка была перенесена фамилия женщины?
4. В городе 10 коммерческих банков. У каждого риск банкротства в течение года составляет 10%. Составьте ряд распределения числа банков, которые могут обанкротиться в течение следующего года; постройте график. Найдите числовые характеристики этого распределения. Запишите в общем виде функцию распределения вероятностей и постройте ее график. Чему равна вероятность того, что в течение года обанкротятся не больше одного банка?
5. Дневная добыча угля в некоторой шахте распределена по нормальному закону с математическим ожиданием 785 т и стандартным отклонением 60 т. Найдите вероятность того, что в определенный день будут добыты, по крайней мере, 800 т угля. Определите долю рабочих дней, в которые будет добыто от 750 до 850 т угля. Найдите вероятность того, что в данный день добыча угля окажется ниже 665 т.
6. По данным выборочного обследования получено следующее распределение семей по среднедушевому доходу. Постройте гистограмму распределения частот. Найдите среднедушевой доход семьи в выборке, дисперсию, среднее квадратическое отклонение, коэффициент вариации. Объясните полученные результаты. |
1. Дискретна випадкова величина
X задана таблицею
розподілу. Знайти М(Х), D(X), σ(X), As, Es, інтегральну функцію F(x)
2. Неперервна випадкова Х величина має щільність ймовірностей. Знайти константу з умови нормування.
Знайти M(X), D(X). |
№1. Припустимо, що події A, B, C означають успішне складання іспиту з "Теорії ймовірностей та математичної статистики" першим, другим і третім студентом відповідно. Записати, в чому полягають події: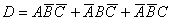 ; ; 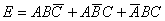
№2. В 3-х банках: "Надра", "Промінвестбанк", "Укрексімбанк" 9 друзів вирішили відкрити по депозитному рахунку. Вважаючи рівно можливим вибір будь-якого банку, знайти ймовірності подій:
а) подія А – у банку "Надра" відкрито рахунок трьома особами;
б) подія В – у одному банку відкрили рахунок рівно 3 особи;
№3. На цирковій виставі рухаються по колу циркового манежу 7 вершників на білих та чорних конях. З них 2 вершники на білих конях. Яка ймовірність того, що вершники на білих конях рухаються один за одним підряд?
№4 На картках написані числа від 60 до 280. Знайти ймовірність того, що число написане на навмання вибраній картці, ділиться:
а) одночасно на 3 та на 5.
б) на 3 або на 5.
№5 У трьох трамвайних вагонах розміщуються 17 пасажирів. Знайдіть ймовірність того, що у першому вагоні розмістяться 7 пасажирів, у другому – 7 пасажирів, у третьому – 3 пасажири.
№6 На потоці 110 студентів: 10 навчається відмінно, 50 – добре, 15 – незадовільно, а решта - трієчники. Ймовірність розв’язання задачі для відмінника – 0,97; для хорошиста – 0,76; для студента, який навчається задовільно – 0,47; для двієчників – 0,16
а) Яка ймовірність розв’язання задачі для навмання обраного студента потоку?
б) Навмання взятий студент не розв’язав задачу. Яка ймовірність, що це хорошист?
№7 Ймовірність того, що впродовж робочого дня не виникне порушень у забезпеченні сировиною дорівнює 0,87. Знайти ймовірність того, що впродовж робочого тижня (5 днів):
а) Порушення будуть впродовж 3 днів;
б) Порушення виникне не більше ніж в 1 день;
в) Знайти найімовірніше число днів без порушень у поставках сировини за робочий місяць (24 дні).
№8 Для вступу до університету необхідно успішно скласти вступні іспити. В середньому їх витримують лише 32 % абітурієнтів. Відомо, що до приймальної комісії подано 2000 заяв. Яка ймовірність того, що принаймні 500 абітурієнтів наберуть прохідний бал?
№ 9 Протягом часу пік (8-00 – 9-30, 17-00 – 19-00) у деякому районі міста відбувається у середньому дві дорожньо-транспортні пригоди за 1 годину.
а) Чому дорівнює ймовірність того, що у деякий день з 8 до 9-30 відбудеться 5 дорожньо-транспортних пригод?
б) Чому дорівнює ймовірність настання 5 дорожньо-транспортних пригод протягом з 17-00 до 19-00?
в) Чому дорівнює ймовірність того, що з 8-00 до 9-30 та з 17-00 до 19-00 однієї доби жодної дорожньо-транспортної пригоди не відбудеться?
№ 10 Дослідний інститут визначив, що 27% виборців підтримують діяльність виконавчої влади. Із великої кількості виборців для участі у телепередачі випадково відібрали 56 осіб. Оцінити ймовірність того, що вибрана доля осіб, які підтримують діяльність виконавчої влади, буде відрізнятись від даних інституту більше ніж на 7%. |
8. Яка ймовірність того, що: а) обидва кролики, носії вірусу В1; б) обидва кролики, носії вірусу В2; в) обидва кролики, носії різних вірусів?
19. До якої групи найбільш ймовірно належить студент.
30. Знайти ймовірність того, що:
а) з 8 насінин зійде 6;
б) з 600 насінин зійде 480;
в) з 600 насінин зійде від 480 до 560;
г) відносна частота насінин, які зійдуть, відхиляється по абсолютній величині від її ймовірності на величину, не більшу за 0,02 при 600.
31. Знайти: а) математичне сподівання; б) дисперсію; в) середнє квадратичне відхилення дискретної випадкової величини X з законом розподілу, який задано в таблиці.
42. Випадкова неперервна величина X має функцію розподілу F(x). Знайти: а) щільність розподілу; б) математичне сподівання; в) дисперсію. Побудувати графіки функції розподілу та щільності розподілу.
53. Визначити: 1) долю насіння, посіяного на глибину менше 4 см; 2) долю насіння, посіяного на глибину менше 2 см.
64.Необхідно: 1) побудувати інтервальний варіаційний ряд розподілу корів за добовим надоєм молока та гістограму відносних частот; 2) побудувати емпіричну функцію розподілу;
75. Необхідно з надійністю 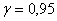 побудувати надійний інтервал для невідомого математичного сподівання a. побудувати надійний інтервал для невідомого математичного сподівання a.
86. Побудувати регресійну модель залежності між товарообігом Z та інтенсивністю потоку покупців P.
97. 1) знайти вибірковий коефіцієнт кореляції між X та Y;
2) записати вибіркове рівняння прямої регресії Y на X;
3) з надійністю 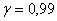 побудувати довірливий інтервал для побудувати довірливий інтервал для 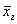 . .
|
1. Скільки різних слів можна скласти з літер вашого а) імені? б) прізвища?
2. Кондуктор автобуса зберігає купюри різної вартості у двох кишенях: в лівій - 7 купюр по 2грн. та 3 купюри по 5 грн., в правій відповідно 12 та 8 купюр. З кожної кишені кондуктор навмання дістає одну купюру. Яка ймовірність того, що: а) обидві купюри однієї вартості? б) купюри різної вартості?
3. На відрізку [-2; 3] навмання вибрано два числа X та Y. Яка ймовірність того, що сума X+Y менша 3, а різниця Y-X менша 2 ?
4. Тираж популярно газети друкується в двох типографіях. Потужності двох типографій відносяться як 3:4, причому перша да 3,5% браку, а друга - 2,5%. Яка ймовірність того, що: а) навмання обраний примірник газети буде бракованим? б) бракований примірник газети надруковано в перший типографії ?
5. Серед 500 коробок взуття нової колекції в 400 лежить взуття чорного кольору. Яка ймовірність того, що у 4 навмання вибраних коробках буде одна з взуттям чорного кольору?
6. У податкових накладних помилки з ймовірністю 5 %. Скільки податкових накладних слід узяти, щоб найімовірніше число накладних без помилок було 70? Яка ймовірність такого числа податкових накладних?
|
1. Бізнесмен проводить чотири фінансові операції з випадковими прибутками (тис. грн.), поданими в таблиці.
По кожній операції бізнесмен несе постійні витрати, подані таблицею.
Потрібно: Побудувати розподіл випадкової величини 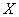 {чистий прибуток}. {чистий прибуток}.
Підрахувати очікуваний середній чистий прибуток (математичне сподівання 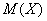 ), дисперсію ), дисперсію 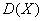 та стандартне відхилення та стандартне відхилення 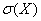 . .
2. Менеджер туристичної компанії виявив, що 30% його клієнтів надають перевагу готелям вищого розряду. Випадковим чином досліджено 8 туристів. Підрахувати ймовірність цієї події:
a) рівно у 5 випадках;
б) число таких випадків знаходиться в межах від 4 до 6.
3. Вага упаковок розфасованого продукту розподілена по нормальному закону із середнім 100 кг і стандартним відхиленням 2 кг. Яка ймовірність, що навмання взята упаковка лежить від 98 до 103 кг.
4. У певний період часу середнє число таксі, що під’їжджають на стоянку на залізничному вокзалі, складає 4 таксі за 5 хвилин. Знайти ймовірність того, що за 5 хвилин під’їде не більше 2 таксі.
5. На біржі було обстежено 600 цінних паперів. За останній місяць 400 з них принесли прибуток. Знайти 95% довірчій інтервал для пропорції прибуткових акцій у генеральній сукупності. |
1. У партії з 10 деталей, 4 браковані. Знайти ймовірність того, що із двох навмання взятих деталей одна стандартна, а одна бракована.
2. На конвеєр подаються деталі з трьох автоматів. Перший дає 90 %, другий – 95 %, а третій 98 % стандартної продукції. Протягом зміни від першого автомата поступає 100 деталей, другого 60 і від третього 40 деталей. Знайти ймовірність попадання на конвеєр стандартної деталі.
3. Задано закон розподілу дискретної випадкової величини.Знайти:
1) значення параметра
2) функцію розподілу, побудувати її графік
3) математичне сподівання та дисперсію випадкової величини
4. Закон розподілу випадкової величини задано функцією розподілу:
Знайти щільність розподілу, та середнє квадратичне відхилення.
5. Випадкова величина розподілена нормально, 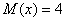 , , 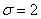 . Знайти імовірності . Знайти імовірності 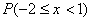 і і 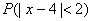 . .
6. За даним статистичним рядом побудувати полігон частот, обчислити 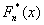 та побудувати графік. та побудувати графік.
7. За даним інтервальним рядом знайти точкові оцінки для математичного сподівання та дисперсії. Вважаючи, що вибірка проведена із нормально розподіленої сукупності з 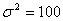 , знайти з надійністю , знайти з надійністю 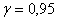 інтервальну оцінку для математичного сподівання сукупності інтервальну оцінку для математичного сподівання сукупності
8. Розв’язати графічним методом:
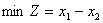 , якщо , якщо 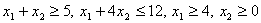 . .
9. Для заданої задачі скласти двоїсту і знайти розв’язок обох задач.
10. Розв’язати транспортну задачу. |
6.1. Дано ймовірності значень випадкової величини: значення 10 має ймовірність 0,3; значення 2 має ймовірність 0,4; значення 8 має ймовірність 0,1; значення 4 має ймовірність 0,2. Побудувати ряд розподілу випадкової величини та многокутник розподілу (полігон).
6.2. Дано ряд розподілу дискретної випадкової величини. Побудувати графік функції розподілу ймовірностей даної випадкової величини.
6.3. Стрілок робить три постріли по мішені. Ймовірність влучення при одному пострілі дорівнює 0,3. Побудувати ряд розподілу числа влучень у мішень.
6.4. В урні 4 кулі з номерами від 1 до 4. Взято дві кулі. Випадкова величина - сума номерів куль. Побудувати ряд розподілу випадкової величини. Знайти функцію розподілу випадкової величини.
6.5. По мішені проведено три постріли. Імовірність влучення в мішень першого пострілу становить 0,1, другого – 0,2, третього – 0,3. Знайти ряд розподілу кількості влучень при трьох пострілах. Побудувати графік розподілу (полігон).
6.6. Серед 5 виробів є один бракований. Щоб його знайти, беруть навмання один виріб за іншим доки не знайдеться бракований. Побудувати ряд розподілу випадкової величини "кількість перевірених виробів".
6.7. Монету кидають 6 разів. Скласти ряд розподілу і побудувати графік розподілу відношення частоти появ герба до числа появ надпису.
6.8. На шляху руху автомобіля 6 світлофорів, кожен з яких дозволяє або забороняє рух автомобіля з ймовірністю 0,5. Скласти ряд розподілу і побудувати функцію розподілу кількості світлофорів, які автомобіль минув до першої зупинки.
6.9. Випадкова величина задана інтегральною функцією. Обчислити імовірність того, що випадкова величина міститься у інтервалі (2,5; 3,5)
6.10. Випадкова величина задана інтегральною функцією. Обчислити імовірність того, що випадкова величина міститься у інтервалі 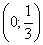 . .
6.11. Випадкова величина задана інтегральною функцією. Знайти щільність розподілу випадкової величини.
6.12. Випадкова величина має закон розподілу зі щільністю.Знайти імовірність того, що випадкова величина попаде у інтервал (1; 2).
6.13. Дано функцію щільності випадково величини. Знайти параметр 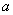 . .
6.14. Випадкова величина задана інтегральною функцією. Звести дану випадкову величину до дискретної та побудувати її ряд розподілу, використовуючи 6 значень дискретної випадкової величини. |
1.22. Гральну кістку підкидають один раз. Яка ймовірність того, що: а) випаде непарне число очок; б) випаде не менше 4 очок; в) випаде не більше 4 очок?
2.22. Підкидають дві гральні кістки, які позначені номерами 1 і 2. Яка ймовірність того, що: а) на першій кістці випаде очок більше ніж на другій; б) на обох кістках випаде однакове число очок.
3.22. Робітник обслуговує три верстати, на яких обробляють однотипні деталі. Ймовірність браку для першого верстату дорівнює 0,02; для другого – 0,03; для третього – 0,04. Оброблені деталі складають в один ящик. Продуктивність праці першого верстата у три рази вища, ніж другого, а третього у два рази менша ніж другого: а) знайти ймовірність того, що навмання взята з ящика деталь бракована; б) деталь яку взяли з ящика виявилась бракованою, знайти ймовірність того, що деталь оброблено на першому, другому і третьому верстатах.
3.22. Робітник обслуговує три верстати, на яких обробляють однотипні деталі. Ймовірність браку для першого верстату дорівнює 0,02; для другого – 0,03; для третього – 0,04. Оброблені деталі складають в один ящик. Продуктивність праці першого верстата у три рази вища, ніж другого, а третього у два рази менша ніж другого: а) знайти ймовірність того, що навмання взята з ящика деталь бракована; б) деталь яку взяли з ящика виявилась бракованою, знайти ймовірність того, що деталь оброблено на першому, другому і третьому верстатах.
4.22. Людина, що належить до певної групи населення, з ймовірністю 0,2 виявляється брюнетом, з ймовірністю 0,3 – шатеном, з ймовірністю 0,4 – блондином і з ймовірністю 0,1 – рудим. Навмання вибирають групу з шести осіб. Знайти ймовірності подій: а) у складі групи не менше 3 блондинів; б) у складі групи хоча б один рудий; в) у складі групи однакове число блондинів і шатенів.
5.22. Серед десяти виготовлених приладів три мають дефект. Знайти закон розподілу і функцію розподілу числа приладів з дефектами серед взятих навмання чотирьох приладів. Обчислити математичне сподівання, дисперсію і середнє квадратичне відхилення цієї випадкової величини.
6.22. Задано вибірку з генеральної сукупності значень дискретної випадкової величини  . Потрібно: а) скласти варіаційний ряд; б) скласти таблицю частот; в) побудувати полігон частот. . Потрібно: а) скласти варіаційний ряд; б) скласти таблицю частот; в) побудувати полігон частот.
7.22. Задано результати 10 спостережень за системою випадкових величин  . Потрібно: а) вважаючи, що залежність між . Потрібно: а) вважаючи, що залежність між  та та  близька до лінійної, знайти за методом найменших квадратів рівняння лінії регресії близька до лінійної, знайти за методом найменших квадратів рівняння лінії регресії  на на  ; б) знайти вибірковий коефіцієнт кореляції ; б) знайти вибірковий коефіцієнт кореляції  . . |
Задача №1. Знайти невизначені інтеграли.
Задача №2. Обчислити визначені інтеграли.
Задача №3. Розв’язати наступні задачі, використовуючи визначений інтеграл:
6. Знайти площу фігури, обмеженої лінією.
Задача №4. Розв’язати наступні задачі, використовуючи визначений інтеграл:
6. Знайти координати центра мас фігури, обмеженої однією аркою циклоїди та віссю Ох.
|
Розрахункова робота № 3
Задача 1. Обчислити невизначений інтеграл
Задача 2. Обчислити визначений інтеграл
Задача 3. Розв’язати задачу Коші |
1. За допомогою таблиці основних інтегралів знайти інтеграли
2. За допомогою методу розкладу знайти інтеграли
3. Підносячи під знак диференціала знайти інтеграли
4. Знайти інтеграли від ірраціональних функцій
5. Знайти інтеграли методом інтегрування за частинами
6. Знайти інтеграли від раціональних функцій
7. Обчислити інтеграли за допомогою формули Ньютона-Лейбніца
8. Чи збіжні інтеграли?
9. Знайти загальний розв’язок диференціального рівняння та його частковий розв’язок що задовольняє початковій умові |
|
|

