|
Задача 1. Имеются выборочные данные о дневной сборке хлопка (X, кг).
|
X
|
20-25
|
25-30
|
30-35
|
35-40
|
40-45
|
|
Число сборщиков
|
8
|
16
|
48
|
16
|
12
|
Вычислить выборочную среднюю, выборочную дисперсию, выборочное среднее квадратическое отклонение этой случайной величины.
Задача 2. Найти доверительный интервал для оценки математического ожидания нормально распределения с надежностью 0,95, зная выборочную среднюю, объем выборки и среднее квадратическое отклонение: 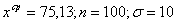 . .
Задача 3. С помощью критерия Пирсона на уровне 0,05 проверить гипотезу о нормальном законе распределения генеральной совокупности Х, если заданы ее эмпирические и теоретические частоты:
|
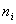
|
9
|
19
|
26
|
34
|
17
|
2
|
|
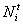
|
12
|
23
|
31
|
24
|
14
|
3
|
Задача 4. Методами корреляционного анализа исследовать зависимость между выпуском продукции Х (тыс. шт.) и себестоимостью одного изделия Y (тыс. руб.) на основе следующих данных. Проверить гипотезу о значимости выборочного коэффициента корреляции при заданном уровне значимости 0,05. Построить линейные уравнения регрессии
|
X
|
2,4
|
6
|
8,6
|
2
|
8
|
3,4
|
|
Y
|
24,5
|
30
|
35
|
18,7
|
42,4
|
18
|
| 
