|
1. Скільки різних слів можна скласти з літер вашого а) імені? б) прізвища?
2. Кондуктор автобуса зберігає купюри різної вартості у двох кишенях: в лівій - 7 купюр по 2грн. та 3 купюри по 5 грн., в правій відповідно 12 та 8 купюр. З кожної кишені кондуктор навмання дістає одну купюру. Яка ймовірність того, що: а) обидві купюри однієї вартості? б) купюри різної вартості?
3. На відрізку [-2; 3] навмання вибрано два числа X та Y. Яка ймовірність того, що сума X+Y менша 3, а різниця Y-X менша 2 ?
4. Тираж популярно газети друкується в двох типографіях. Потужності двох типографій відносяться як 3:4, причому перша да 3,5% браку, а друга - 2,5%. Яка ймовірність того, що: а) навмання обраний примірник газети буде бракованим? б) бракований примірник газети надруковано в перший типографії ?
5. Серед 500 коробок взуття нової колекції в 400 лежить взуття чорного кольору. Яка ймовірність того, що у 4 навмання вибраних коробках буде одна з взуттям чорного кольору?
6. У податкових накладних помилки з ймовірністю 5 %. Скільки податкових накладних слід узяти, щоб найімовірніше число накладних без помилок було 70? Яка ймовірність такого числа податкових накладних?
7. Імовірність прийняття на роботу кожного з 5 претендентів становить 0,2. Випадкова величина X - число претендентів, прийнятих на роботу. Знайти закон розподілу випадково велечини X, математичне сподівання MX, дисперсію DX, середньоквадратичне в дхилення.
8. Випадкова величина X задана функцію розподілу 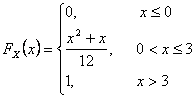
Визначити щільність розподілу f(x), математичне сподівання MX, дисперсію DX. Знайти ймовірність того, що X набуде значення з інтервалу [0;2). Побудувати графіки функцій 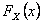 та f(x). та f(x).
9. Знайти вибіркове середнє, дисперсію, моду та медіану для вибірки:
|
xi
|
1
|
2
|
3
|
4
|
5
|
|
ni
|
2
|
5
|
6
|
8
|
4
|
Побудувати емпіричну функцію розподілу, гістограму та полігон частот.
10. Знайти рівняння лінійної рересіїї та обчислити вибірковий коефіцієнт кореляції за вибіркою:
|
xi
|
7
|
9
|
11
|
14
|
15
|
|
yi
|
5
|
10
|
15
|
19
|
23
|
| 
